El álgebra Boleana consiste en utilizar literales en lugar de combinaciones de "unos" y "ceros" para el análisis de los circuitos lógicos. Empezaremos por considerar la función NOT junto con su Tabla de Verdad:
Aquí hemos prescindido temporalmente del triángulo porque en los diagramas de circuitos lógicos es la burbuja la que representa la inversión de la entrada. Obsérvese que la entrada es A y la salida es C, y la salida es llamada la negación de A (la inversión de su valor), con el efecto representado con una línea horizontal puesta sobre el símbolo A.
Puesto que la salida del NOT es siempre el inverso lógico de la entrada A, podemos representar la salida del NOT como:
Salida = A
con lo cual con la barra horizontal puesta encima queremos decir que la salida es el inverso o el complemento de la entrada. Esto se lee puede leer de diversas maneras tales como "el inverso de A", "el complemento de A", o "A negado", todas ellas equivalentes. En este libro, siempre y cuando ello ha sido posible, se ha hecho además otra cosa con fines didácticos: se ha escrito el símbolo de una variable invertida lógicamente con color azul. Además, por las dificultades tipográficas para poder representar símbolos con una barra horizontal puesta encima de ellos, en muchos libros y muchos monitores de computadora con ciertas combinaciones de sistemas operativos y navegadores de Internet se hace preferible o inclusive mandatorio recurrir a otro tipo de representación por medio del apóstrofe ('). Bajo esta representación, algo que tiene puesto un apóstrofe inmediatamente a su derecha se debe tomar como una variable invertida en el sentido Boleano. Si el apóstrofe está puesto inmediatamente a la derecha de una expresión entre paréntesis, entonces toda la expresión entre paréntesis se debe considerar negada lógicamente. Todo esto quiere decir que en este libro las siguientes expresiones deben tomarse como completamente equivalentes:
A = A'
A + B = (A + B)'
A • B = (A • B)'
ā = (a')'
A + B = (A + B)'
A • B = (A • B)'
ā = (a')'
Siempre y cuando sea posible o conveniente, cuando se escriban variables negadas se utilizarán ambos sistemas de notación para que el lector se vaya acostumbrando al uso de los dos sistemas tipográficos.
Consideremos ahora la función OR junto con su Tabla de Verdad:
Obsérvese en la Tabla de Verdad cómo la salida del OR asemeja la suma de los valores a sus entradas. Por ejemplo, en el primer renglón tenemos que cero (0) más cero (0) es igual a cero (0). En el segundo renglón tenemos que cero (0) más uno (1) es igual a uno (1), y en el tercer renglón también tenemos que uno (1) más cero (0) es igual a uno (1). Guiados por esta observación, podemos postular que la salida del OR será igual a algo que llamamos la suma lógica de los valores a sus entradas, o sea:
Salida = A + B
Tal vez el lector ya se haya dado cuenta de que, según lo que podemos ver en el cuarto renglón de la Tabla de Verdad, uno (1) más uno (1) es igual a uno (1), o sea:
1 + 1 = 1
Esta relación puede dejar perplejos a muchos a primera vista. Es aquí cuando se le advierte al lector que una cosa es la suma lógica de dos variables llevada a cabo con un bloque OR, y otra cosa muy diferente es la suma binaria de dos variables. La suma lógica o suma Boleana de 1 y 1 es igual a 1, mientras que la suma binaria de 1 y 1 será igual (en el sistema de numeración binaria) a 10.
Sobre esto último debemos recordar que estamos manejando un álgebra diferente al álgebra clásica. Debemos, por lo tanto, adaptar nuestra mente a las estructuras matemáticas requeridas para el estudio de los circuitos lógicos, porque es el álgebra Boleana y no nuestra álgebra clásica el "álgebra" que entienden las máquinas en su mundo de "encendidos" o "unos" y "apagados" o "ceros". El descubrimiento de este hecho por Claude Shannon fue lo que posibilitó el manejo matemático adecuado de los circuitos lógicos, los cuales se llaman así porque son circuitos cuyo comportamiento es descrito con las leyes de la lógica simbólica (utilizadas originalmente para el estudio de los pensamientos humanos en cuanto tales sin ninguna referencia a circuitos eléctricos) asentadas por George Boole.
Pasamos a estudiar ahora la función AND con su Tabla de Verdad:
Obsérvese en la Tabla de Verdad cómo la salida C del bloque AND asemeja el producto de los valores a sus entradas A y B. Por ejemplo, en el primer renglón tenemos que cero (0) por cero (0) es igual a cero (0). En el segundo renglón tenemos que cero (0) por uno (1) sigue siendo igual a cero (0). En el tercer renglón también seguimos teniendo que uno (1) por cero (0) es igual a cero (0). Es en el cuarto renglón en donde tenemos que uno (1) por uno (1) es igual a uno (1). Guiados por esta observación, podemos asegurar que la salida del AND es igual al producto de los valores de las entradas, o sea:
Salida = A • B
En el álgebra Boleana, hay además una serie de teoremas relativamente fáciles de demostrar (esto se lleva a cabo en la sección de problemas resueltos), que son los siguientes:
(1) A + 1 = 1Usando los resultados anteriores, se puede analizar cualesquier circuito lógico y, muy a menudo, simplificarlo. Por ejemplo, supóngase que un circuito lógico tiene la siguiente salida:
(2) A • 1 = A
(3) A + 0 = 0
(4) A • 0 = 0
(5) A + A = A
(6) A • A = A
(7) ā = a
(8) A + A = 1
(9) A • A = 0
AB + B + C + CD
El primer paso es factorizar los términos comunes como se muestra a continuación:
(A + 1) • B + (C + 1) •D
Usando el primer teorema de los dados arriba, esta expresión se reduce de inmediato a lo siguiente:
B + D
Se ve claramente que es más fácil y económico construír el circuito usando esta última expresión (sólo se requiere un OR de dos entradas) que usando la expresión original con la cual se requieren dos bloques AND y un OR de cuatro entradas.
Anteriormente, al carecer de los recursos del álgebra Boleana, la única manera de descubrir el comportamiento de un circuito lógico construído a partir de las tres funciones lógicas básicas era aplicar en las entradas todas las combinaciones posibles de "unos" y "ceros" y rastrear los cambios para cada una de estas combinaciones a lo largo del circuito obteniendo las salidas resultantes, y con ello construír una Tabla de Verdad. Y no había una forma obvia de poder simplificar el circuito reduciendo el número de componentes requeridos para su construcción. Pero ahora, con el recurso del álgebra Boleana en nuestras manos, en vez de rastrear a lo largo de un circuito lógico todas las combinaciones posibles de "unos" y "ceros" hasta llegar a la salida del circuito, podemos rastrear el efecto de los componentes sobre las variables simbólicas a la entrada, y sin necesidad de recurrir a los "unos" y "ceros" podemos incluso intentar llevar a cabo una simplificación del circuito que antes no estábamos posibilitados para hacer. A continuación tenemos un ejemplo de cómo podemos "rastrear" las entradas hasta llegar a la salida de un circuito lógico para obtener una expresión simbólica para su salida en función de las variables de entrada:
Podemos ver cómo en el AND que está en el extremo izquierdo del diagrama, las variables de entrada B y C son puestas en la salida del mismo como BC, y esto sirve como una de las entradas al NOR en la parte superior del diagrama, el cual suma (en el sentido Boleano) BC a la otra entrada A, llevando a cabo inmediatamente tras esto la inversión lógica para obtener la expresión A+BC a la salida de dicho NOR. Por otro lado, el NAND que está situado debajo de este NOR recibe como entrada a la señal que le llega de la terminal A junto con la señal que le llega de la terminal B procesada previamente por el inversor NOT, de modo tal que las dos entradas a este NAND son A y B. El NAND procesa estas dos entradas llevando a cabo primero el proceso de multiplicación (en el sentido Boleano) de estas entradas produciendo el término AB, el cual es invertido inmediatamente por la burbuja inversora del NAND convirtiéndose en el término mostrado en el diagrama. Continuando el rastreo de las variables simbólicas, llegamos hasta la expresión final de la salida Q, la cual ciertamente parece ser una expresión susceptible de ser simplificada mediante álgebra Boleana.
Un concepto importante en nuestro estudio es el concepto del minterm, el cual nos permite obtener la expresión de salida para un circuito a partir de su Tabla de Verdad.
Considérese un circuito cuya Tabla de Verdad sea la siguiente:
Concentremos nuestra atención en aquellas salidas que tengan el valor de 1. En este caso, son las salidas f2 y f3.
Por definición, un minterm correspondiente a la salida de un circuito es igual al producto de las literales A y B que representan las variables de entrada de modo tal que se produzca una salida de 1. En el segundo renglón de la Tabla de Verdad, puesto que A=0 hay que invertir A para que su producto con B=1 produzca una salida de 1. De este modo, vemos que el primer minterm es:
f2 = A B___[ = A' B ]
Usando el mismo razonamiento, el segundo minterm será:
f3 = A B_____[AB']
Recurrimos ahora a un teorema fundamental (la demostración no es difícil pero no se llevará a cabo en este libro para beneficio de quienes las demostraciones matemáticas no es su fuerte) que nos dice que la salida de un circuito lógico es igual a la suma de los minterms de su Tabla de Verdad.
Entonces, la salida del circuito en este caso será:
Salida = f2 + f3
Salida = A B + A B
Salida = A B + A B
Otro concepto importante es el concepto del maxterm.
Considérese un circuito lógico cuya Tabla de Verdad es la siguiente:
Concentramos ahora nuestra atención en aquellas salidas que son cero. En este caso, son las salidas f2 y f4 .
Por definición, un maxterm correspondiente a la salida de un circuito es igual a la suma de las literales A y B que representan las variables de entrada de modo tal que se produzca una salida de 0 (compárese con la definición del minterm). En el segundo renglón de la Tabla de Verdad, puesto que B=1, hay que invertir la variable B para que su suma con A=0 produzca una salida de 0. De este modo, vemos que el primer maxterm es:
f2 = A + B
Usando el mismo razonamiento, el segundo maxterm será:
f4 = A + B
Recurrimos ahora a otro teorema fundamental de la teoría de los circuitos lógicos que nos dice que la salida de un circuito lógico es igual al producto de los maxterms de su Tabla de Verdad.
La salida del circuito lógico en este caso será:
Salida = f2 • f4
Salida = ( A + B) • (A + B)
Salida = ( A + B) • (A + B)
Podemos remover los paréntesis y simplificar esta expresión llevando a cabo las multiplicaciones requeridas en forma parecida a la forma en la cual estamos acostumbrados en el álgebra tradicional:
Salida = AA + AB + A B + B B
Según uno de los teoremas enunciados anteriormente:
A • A = 0
y aplicando otro de los teoremas se tiene que:
B • B = B
Tenemos entonces que la salida se reduce a:
Salida = AB + A B + B
Podemos factorizar los primeros dos términos como sigue:
Salida = (A + A)•B + B
Usando el teorema que nos dice que A + A = 1, la expresión se simplifica a:
Salida = B + B
Pero otro de los teoremas nos dice que cualquier variable lógica sumada a sí misma nos produce la misma variable (este teorema aplica por igual a todas las variables, así se trate de variables invertidas), o sea el teorema:
A + A = A
Entonces la expresión final se reduce simplemente a:
Salida = B
Entonces el circuito de dos entradas A y B representado por la última Tabla de Verdad lo único que hace es invertir la entrada B e ignorar la entrada A. Es, en esencia, simplemente un inversor conectado a la señal lógica B. Una nueva inspección a la Tabla de Verdad nos confirma esto que al principio no nos era tan obvio.
Podemos, por lo tanto, obtener la expresión de salida para cualesquier circuito lógico a partir de su Tabla de Verdad ya sea por medio de minterms o por medio de maxterms. La decisión de utilizar minterms o maxterms es meramente una cuestión de conveniencia. Por ejemplo, si la Tabla de Verdad para un circuito tiene menos minterms que maxterms, posiblemente usando minterms se llegue más rápidamente a una expresión final.
Por último, vamos a estudiar el concepto del diagrama de tiempos, el cual siempre se lee de izquierda a derecha.
Supóngase que con el transcurso del tiempo, un circuito lógico produce la siguiente salida en tiempos igualmente espaciados tn:
En el transcurso del tiempo de t1 a t2, la salida es 1. En el transcurso del tiempo t2 a t3, la salida es 0. Podemos ver cómo en el transcurso del tiempo t1 a t3 se habrá formado la palabra:
10
En el transcurso del tiempo t3 a t4 la salida es 1. Y en el transcurso del tiempo t4 a t5 la salida también es 1. Vemos que en el transcurso del tiempo t1 a t5 se habrá formado la palabra:
1011
Así, desde el inicio del tiempo t1 hasta el final del tiempo t10 se habrá formado la palabra:
101101001
En general, dado un diagrama de tiempos podemos obtener a partir del mismo la palabra binaria que éste genera siempre y cuando estemos seguros del espaciamiento de tiempos entre un "bit" y el que le sigue. La división precisa del tiempo es crucial para poder fijar y distinguir en forma correcta los "unos" y los "ceros". En el caso que acabamos de ver, si la división del tiempo cronometrada en cierto sistema digital fuera el doble de lo que acabamos de ver, entonces en lugar de la palabra 1011 generada desde el comienzo de t1 hasta el final de t5 podríamos muy bien haber tenido la palabra 11001111. Y si fuera el triple, entonces la palabra debería haber sido 111000111111. Este detalle se vuelve mucho más importante cuando la palabra binaria que está siendo enviada o procesada es una palabra que consta de puros "unos" (como 11111111) o de puros "ceros" (como 00000000) porque en tal caso la misma palabra no nos proporciona absolutamente ninguna pista sobre cuántos "bits" la forman.
Así como podemos obtener de un diagrama de tiempos la palabra binaria mostrada por dicho diagrama, de la misma manera dada una palabra binaria podemos obtener a partir de la misma el diagrama de tiempos que la produce. Por ejemplo, el diagrama de tiempos de la palabra:
11011101
será como se muestra a continuación:
Con mucha frecuencia en el estudio y análisis de sistemas digitales, los diagramas de tiempo se presentan como diagramas de tiempos múltiples, sincronizados. Esto quiere decir que en lugar de un solo diagrama podemos tener dos, tres, o más diagramas, alineados uno encima del otro de tal modo que sus tiempos se correspondan mutuamente. A continuación tenemos un diagrama de tiempos múltiple de un circuito digital que posee cuatro salidas en lugar de una sola, designadas como Q0, Q1, Q2 y Q3:
Aunque a primera vista no lo parezca, el circuito que produce este diagrama de tiempos múltiple está llevando a cabo una labor muy importante. Podemos entender mejor lo que está sucediendo si acomodamos las salidas de modo tal que se forme la palabra binaria:
Q3Q2Q1Q0
Veamos ahora lo que va sucediendo conforme el tiempo va transcurriendo de izquierda a derecha, veamos las palabras binarias que se van formando empezando por la primera:
Q3Q2Q1Q0 = 0000
Q3Q2Q1Q0 = 0001
Q3Q2Q1Q0 = 0010
Q3Q2Q1Q0 = 0011
Q3Q2Q1Q0 = 0100
∙ ∙ ∙
Posiblemente a estas alturas ya sea obvio lo que está realizando el circuito lógico que produce este diagrama de tiempos. Es un contador binario de conteo ascendente. Está contando hacia arriba en el lenguaje propio de las máquinas electrónicas, en el lenguaje binario de "unos" y "ceros".




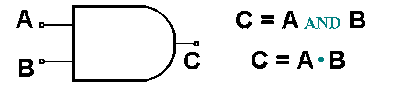









No hay comentarios:
Publicar un comentario
ESCRIBE AQUI TUS COMENTARIOS Y DEJA TAMBIEN TUS DUDAS E INTERESES QUE TE CONTESTARÉ A LA MAYOR BREVEDAD POSIBLE. SI TE INTERESA CUALQUIER OTRO TEMA PREGUNTAMELO QUE TE AYUDARÉ .