FUERZA ENTRE CARGAS

Coulomb fue el primero en determinar, en 1785, el valor de las fuerzas ejercidas entre cargas eléctricas. Usando una balanza de torsión determinó que la magnitud de la fuerza con que se atraen o repelen dos cargas eléctricas puntuales en reposo es directamente proporcional al producto de las magnitudes de cada carga e inversamente proporcional al cuadrado de la distancia que las separa.

donde q₁ y q₂ son las cargas, r es la distancia que las separa y la constante de proporcionalidad k depende del sistema de unidades.

Una propiedad fundamental de estas fuerzas es el principio de superposición que establece que, cuando hay varias cargas q_j, la fuerza resultante sobre una cualquiera de ellas es la suma vectorial de las fuerzas ejercidas por todas las demás. La fuerza 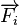ejercida sobre la carga puntual q_i en reposo está dada en el SI por:

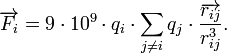
donde denota el vector que une la carga q_j con la carga q_i.

Cuando las cargas están en movimiento aparecen también fuerzas magnéticas. La forma más sencilla de describir el fenómeno es con el uso de campos eléctrico () y magnético (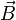), de los que a su vez se pueden derivar las fuerzas a partir de la fórmula de Lorentz:

En el caso general de cargas distribuidas de manera arbitraria, no es posible escribir expresiones explícitas de las fuerzas. Hay que resolver las ecuaciones de Maxwell, calcular los campos y derivar las fuerzas a partir de las expresiones de la energía electromagnética.